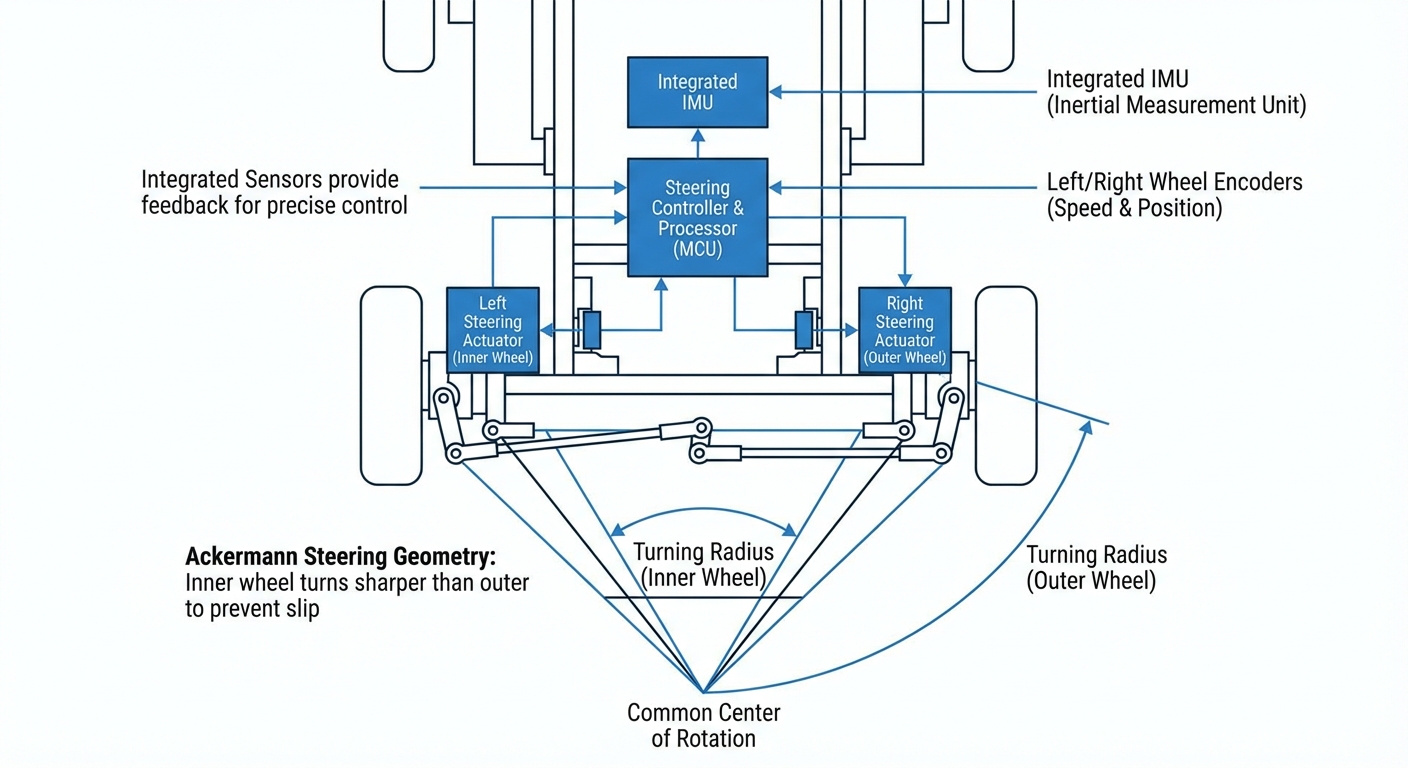
Ackermann Steering Geometry
Unlock pinpoint maneuverability for your autonomous mobile robots. Ackermann geometry makes every wheel follow a perfect concentric circle around one turn center, ditching tire scrubbing and boosting traction for heavy-payload AGVs.

Core Concepts
Instant Centre of Rotation
It's the spot where all the extended wheel axes meet. This setup lets the robot turn smoothly without any sideways wheel slip.
Inner vs. Outer Angles
On a curve, the inner wheel travels a shorter path than the outer one. Ackermann geometry angles the inner wheel more sharply to make up for it.
Eliminating Scrubbing
Parallel steering makes tires drag sideways (that's scrubbing) in turns. Ackermann fixes this, slashing tire wear and energy use on AGVs.
Kinematic Stability
It delivers rock-solid stability at higher speeds compared to differential drive, perfect for logistics bots hauling sensitive or shaky loads.
Electronic Differential
Today's robotics often swap mechanical linkages for software-driven independent steering motors, nailing ideal Ackermann angles on the fly.
Path Planning
Unlike holonomic drives, Ackermann systems have non-holonomic constraints. That means you need tailored path planning like Reeds-Shepp for smooth navigation.
How It Works
Ackermann steering boils down to one key idea: for no-slip turning, every wheel must roll in a circle around the same center point.
In a typical 4-wheel AGV setup, this point—the Instant Centre of Rotation—sits on the extended rear axle line. So the front inner wheel steers sharper (${\delta}_{i}$) than the outer one (${\delta}_{o}$).
The math is $\cot {\delta}_{o} - \cot {\delta}_{i} = \frac{w}{l}$, with $w$ as track width and $l$ as wheelbase. Stick to this, and your controllers can sync steering motors perfectly, cutting stress and battery drain.
Real-World Applications
Heavy-Duty Logistics
You'll see it in big forklifts and pallet movers, where tire scrub would chew through wheels fast and scar warehouse floors under multi-ton loads.
Automotive Manufacturing
Automated Guided Carts hauling car chassis use Ackermann to track magnetic tape or vision lines with dead-on precision and stability.
Hospital Delivery Robots
Service robots in quiet spaces love Ackermann—it stops the annoying 'squeak' from tire scrubbing during corridor turns.
Outdoor Agriculture
Autonomous tractors and harvesters count on it to keep soil intact, avoiding wheel-tear during those tight headland maneuvers.
Frequently Asked Questions
What is the main advantage of Ackermann steering over differential drive?
The big win is stability and traction at higher speeds. Differential drive is simpler but burns energy on wheel slip and wears tires quick. Ackermann keeps all wheels rolling cleanly, ideal for heavy loads on steady surfaces.
Can an AGV with Ackermann steering rotate in place?
No, standard Ackermann can't do zero-radius turns (like spinning on a dime). There's a minimum radius based on max inner-wheel steer and wheelbase. For that, go skid-steer or omnidirectional.
How is Ackermann geometry implemented in modern electric robots?
Traditionally, mechanical linkages and tie rods handled it. Now robotics leans on 'Electronic Ackermann' or 'Steer-by-Wire'—servos per wheel controlled by software for less hardware and easy tweaks.
Does the payload weight affect the steering geometry?
The geometry stays the same, but tires deform more (slip angle) under heavy loads. Smart AGV controllers tweak the Ackermann math for slip to keep trajectories spot-on.
What is the "Jeantaud Diagram"?
The Jeantaud diagram is a handy graph for nailing steering linkage geometry. It shows lines from steering pivots to the rear axle center, ensuring wheels point right at the Instant Centre of Rotation.
Is Ackermann steering suitable for off-road robotics?
Yes, it's common in ag and outdoor survey bots. Skid-steering rules rough terrain, but Ackermann shines when you need to protect the soil from turn-induced damage.
How does path planning differ for Ackermann vs. Differential drive?
Ackermann bots are non-holonomic—no sideways moves or instant turns. Planners must respect the min turning radius with gentle curves like Dubins or Reeds-Shepp, not the sharp pivots differential drive allows.
What is Reverse Ackermann geometry?
In racing, 'Reverse Ackermann' (outer wheel steers more) handles big slip angles at speed. But for low-to-mid-speed industrial AGVs and robots, standard Ackermann (or Pro-Ackermann) is the efficiency champ.
Does Ackermann steering increase the cost of the robot?
Usually, yeah. It needs steering gear (motors, rack-and-pinion, actuators) on top of drive motors. Differential is cheaper with just two fixed ones. But savings on tires and floor fixes often pay it back.
How do I calculate the steering angle for my robot?
Know your target radius $R$ and wheelbase $L$? Inner angle is $\arctan(L / (R - W/2))$, outer is $\arctan(L / (R + W/2))$, with $W$ as track width. Crucial for your motion controller code.
Can Ackermann steering be combined with 4-wheel drive?
Totally. Lots of outdoor rovers pair 4WD with Ackermann. An electronic differential is key so outer wheels speed up to match the geometry's path differences.
What is Double Ackermann steering?
Double Ackermann means 4-wheel steering where front and rear axles turn opposite ways. This slashes turning radius while keeping all wheels circling one common center.