A* Path Planning
The gold standard algorithm for autonomous navigation, allowing AGVs and mobile robots to calculate the most optimal route in complex environments. By balancing actual path costs with heuristic estimates, A* ensures your fleet moves with mathematical precision and efficiency.

Core Concepts
f(n) Score
The total estimated cost of a path going through node 'n'. It is calculated as f(n) = g(n) + h(n), driving the search direction toward the goal.
Grid Occupancy
The environment is divided into a discrete grid. Cells are marked as either 'traversable' or 'blocked' based on mapping data from LIDAR or cameras.
Heuristics (h)
The estimated cost from the current node to the goal. Common methods like Manhattan or Euclidean distance guide the algorithm to ignore irrelevant paths.
Open Set
A priority queue containing nodes that have been discovered but not yet evaluated. The node with the lowest f-score is always processed next.
Cost to Here (g)
The exact cost of the path from the start node to the current node 'n'. This accounts for distance traveled and terrain difficulty penalties.
Optimal Path
By back-tracking from the goal to the start node via the 'parent' pointers, A* reconstructs the shortest possible path without colliding with obstacles.
How It Works
A* is an informed search algorithm, meaning it searches for paths efficiently by using knowledge about the goal's location. Unlike Dijkstra's algorithm, which expands in all directions equally, A* is directional. It prioritizes nodes that appear to lead closer to the destination, drastically reducing computation time.
The algorithm maintains two lists: the Open Set (candidates for exploration) and the Closed Set (already evaluated). At each step, it selects the node with the lowest f(n) score from the Open Set. It then explores the neighbors of that node, calculating their costs and adding them to the queue.
For mobile robots and AGVs, this logic is applied to a navigation grid or mesh. Walls, shelving units, and no-go zones are treated as blocked nodes. The result is a coordinate-by-coordinate plan that the robot's motion controller can execute to reach the destination safely.
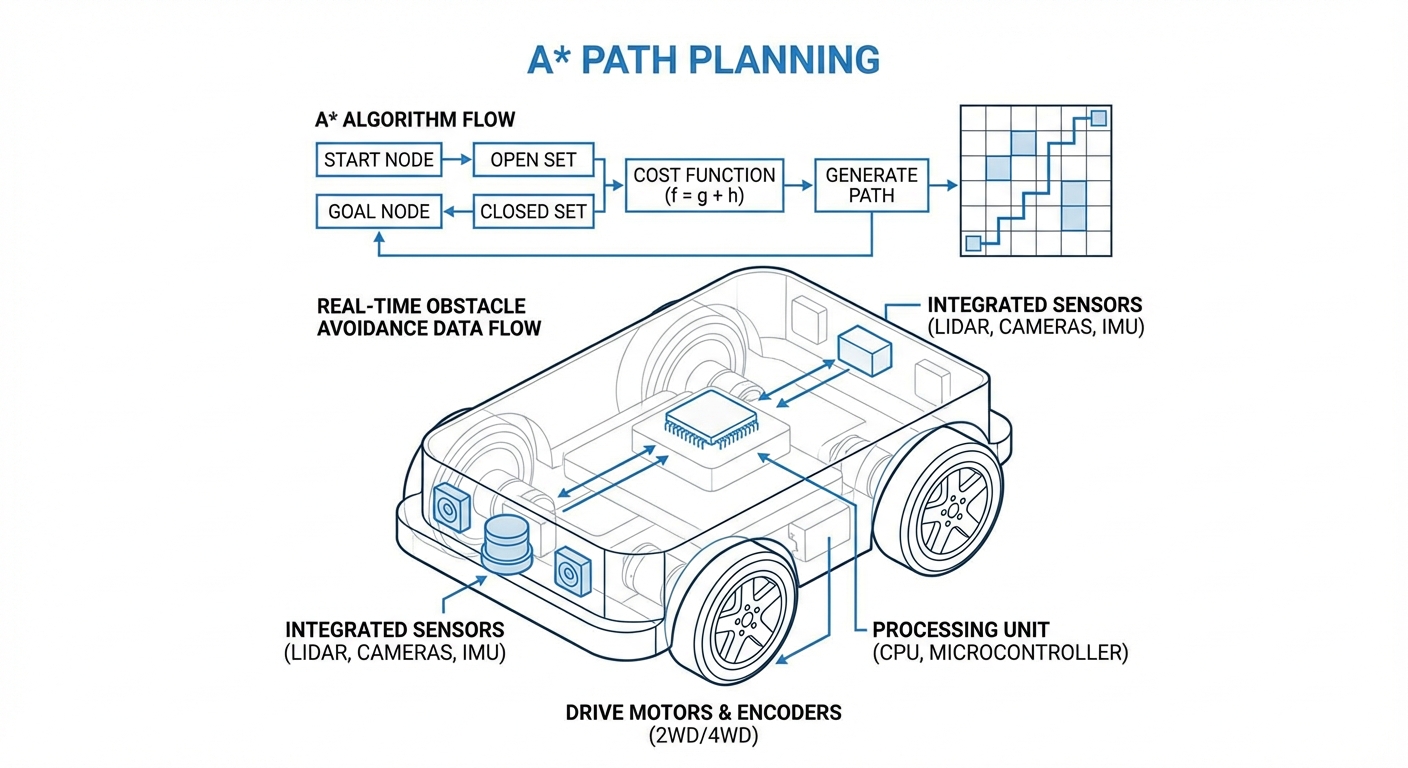
Real-World Applications
Automated Warehousing
AGVs utilize A* to navigate vast warehouse grids, calculating the fastest route from charging stations to picking zones while dynamically avoiding shelving units and other active robots.
Hospital Logistics
Delivery robots use path planning to transport linens and medicine through complex hospital corridors, respecting strict "keep-out" zones and prioritizing clear hallways over crowded lobbies.
Flexible Manufacturing
In Industry 4.0 factories, AMR fleets deliver raw materials to assembly lines just-in-time. A* allows for rapid re-routing if a forklift blocks a primary aisle, ensuring production continuity.
Last-Mile Delivery
Sidewalk robots employ advanced variations of A* to navigate urban environments, calculating paths that adhere to sidewalk boundaries while handling static obstacles like street lamps and benches.
Frequently Asked Questions
What is the main advantage of A* over Dijkstra's algorithm?
The main advantage is efficiency. While Dijkstra's algorithm guarantees the shortest path, it explores in all directions uniformly. A* uses a heuristic function to estimate the distance to the goal, directing the search towards the target and significantly reducing the number of nodes that need to be evaluated.
Does A* guarantee the shortest path?
Yes, A* is guaranteed to find the shortest path provided that the heuristic function used is "admissible." An admissible heuristic never overestimates the cost of reaching the goal. If the heuristic overestimates, the algorithm runs faster but may settle for a sub-optimal path.
How does A* handle dynamic obstacles like moving people?
Standard A* calculates a global path based on a static map. To handle dynamic obstacles, robots often use a local planner (like DWA) for immediate avoidance or employ variations like D* Lite or A* Replanning, which can rapidly update the path when the environment changes without recalculating from scratch.
Which heuristic function should I use for grid-based movement?
If your robot can move in 4 directions (up, down, left, right), Manhattan distance is the standard choice. If diagonal movement is allowed (8 directions), Octile or Chebyshev distance is preferred. For any-angle movement, Euclidean distance is typically used.
What happens if no path exists to the destination?
If the Open Set becomes empty and the goal has not been reached, the algorithm terminates and reports that the destination is unreachable. This prevents the robot from entering an infinite loop or attempting to drive through walls.
Is A* computationally expensive for large warehouses?
It can be memory-intensive on very large, high-resolution grids because it must store nodes in the Open and Closed sets. Techniques like Jump Point Search (JPS) or Hierarchical Pathfinding (HPA*) are often used to optimize A* for large-scale maps by breaking the problem down into smaller clusters.
How do we handle robot size and turning radius?
Standard A* treats the robot as a point. To account for size, we "inflate" the obstacles in the map by the robot's radius (creating a Configuration Space). For turning radius constraints (non-holonomic robots), Hybrid A* is used, which includes the vehicle's orientation and kinematic constraints in the node state.
Why does the path sometimes look "jagged" or "blocky"?
Since A* typically operates on a grid, the raw path is a sequence of grid cell centers, resulting in zig-zag movements. Path smoothing algorithms (like Bézier curves or string pulling) are applied post-process to create fluid, drivable trajectories for the robot.
Can A* handle different terrain costs (e.g., mud vs. concrete)?
Absolutely. The 'g' cost function can be modified to include terrain penalties. For example, moving through a 'mud' cell might cost 5x more than a 'concrete' cell. A* will naturally route around the difficult terrain unless the detour is significantly longer than driving through it.
Does A* work in 3D environments (drones/manipulators)?
Yes, A* is dimension-agnostic. It works in 3D grids (voxels) for drones or high-dimensional spaces for robotic arms (degrees of freedom). However, the search space grows exponentially with dimensions, so sampling-based planners like RRT* are sometimes preferred for high-DOF arms.
What is Theta*?
Theta* is a variant of A* that allows for "any-angle" path planning on a grid. Instead of constraining movement strictly to grid edges, it checks for line-of-sight between non-adjacent nodes, producing smoother and shorter paths that don't conform artificially to the grid axes.
How do I implement A* in Python or C++?
Implementation requires a Priority Queue data structure to manage the Open Set efficiently. Python's `heapq` module or C++'s `std::priority_queue` are standard tools. You will need a class for Nodes to store position, parent, and f, g, h scores, and a loop to process the lowest f-score node until the goal is found.